押尾 FP3級への道（6種類の係数）

押尾と6種類の係数

どうも。押尾センパイです。

前回に引き続き、FP3級試験の問題演習をしながら試験に出る用語をおぼえていきます。
今回は、ライフプランニングと資金計画分野で超頻出の6種類の係数をマスターします！

6種類の係数とは…

終価係数
現価係数
年金終価係数
減債基金係数
年金現価係数
資本回収係数

漢字だらけで舌を噛みそうなものばかり。
しかし、これをおぼえないと、得点源である計算問題を解くことができません。
気合を入れてがんばるぞ！

6種類の係数のおぼえかた

押尾、6つの係数を丸暗記しようと考えました。
しかし、名前が似ているため頭が混乱してしまい、うまくおぼえられません。

みやこ：だいぶ苦戦してるな…
押尾：似たような名前なんで、おぼえてもすぐ忘れてしまうんですよ。困ったなあ。
みやこ：ただ暗記しても記憶が定着しないよ。「何の金額を求める係数なのか」を考えないと。
押尾：う～ん。
みやこ：こういうのは、文字だけ見ててはダメ！イメージでおぼえないと。

困っている押尾を見かねたのか、みやこさんが図を描いてくれました。

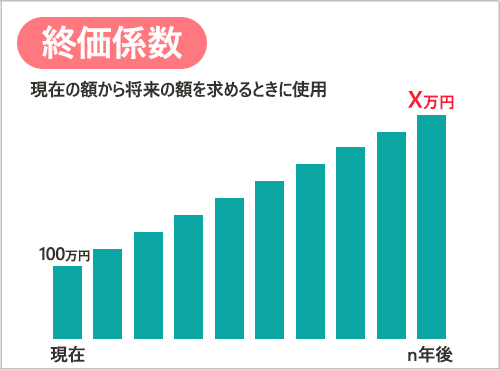
みやこ：終価係数は、いまあるお金を一定期間、一定の利率で複利運用したら、将来いくらになるかを求める係数。運用した「終わりの価格」ってこと。
押尾：ふむふむ。終わりの数字を求めるんですね

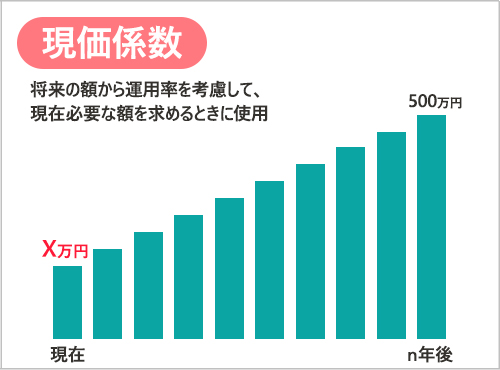
みやこ：現価係数はその逆で、一定期間、一定の利率で複利運用して目標額に到達したい場合、いまいくらあればいいかを求める係数。「現在の価格」ってこと。
押尾：こっちは、はじめの数字を求めるのか！

みやこ：終価係数と現価係数は、運用グループとおぼえよう。

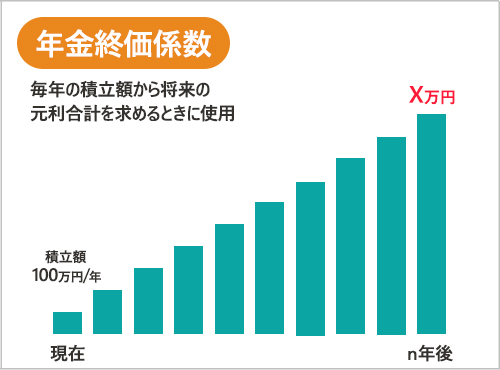
みやこ：続いて年金終価係数。終価とあるから、将来いくらになるかを求める係数だね。
押尾：ん！？さっきとどう違うんだろう？
みやこ：これは、（持っているお金がゼロの状態から）一定期間、一定額の積み立てをして、一定利率の複利で運用したら、将来いくらになるかを求める係数。
押尾：あ、なるほど。

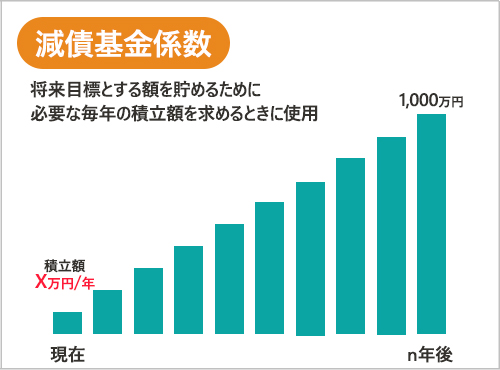
みやこ：これの逆が減債基金係数。一定期間、一定の利率で複利運用をして目標額に到達するためには、毎回いくら積み立てればいいかを求める係数だね。
押尾：減債基金係数ってわかりにくいですね。
みやこ：「源さん、毎回いくら積み立てるの？」っておぼえておこう。
押尾：そんなんでいいんですか？

みやこ：年金終価係数と減債基金係数は、積立グループとおぼえよう。

みやこ：運用、積立ときて、つぎは取り崩し。
押尾：取り崩すということは、お金が減っていくんですね。
みやこ：そのとおり。
押尾：やばい。オレ、冴えてる！

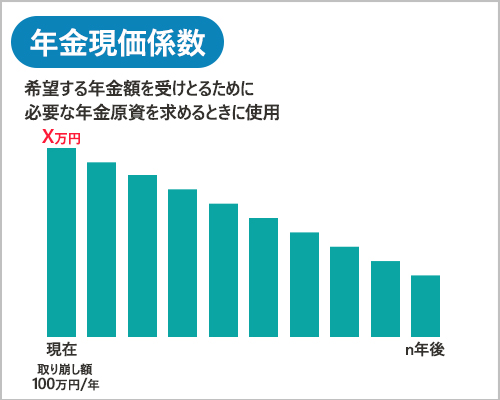
みやこ：まずは年金現価係数から。現価だから、いまいくらあればいいかを求める係数だね。
押尾：ひょっとして、毎回取り崩すためには、いまいくらあればいいかってことですか？
みやこ：押尾、ホントに冴えてるね！年金現価係数は、一定期間、一定利率の複利で運用しながら、毎回一定額を取り崩す場合、いまいくらあればいいかを求める係数だよ。

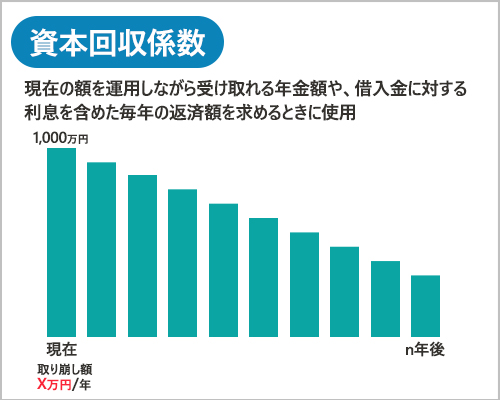
押尾：ということは、資本回収係数は、年金現価係数の逆になるんですね。
みやこ：そう！
押尾：え～と、「いまあるお金を一定期間、一定利率の複利で運用したら、毎回いくら取り崩せるか」を求める係数ですね。
みやこ：押尾、やるね～。住宅ローン等を返済する場合、毎回の返済額がいくらかを求めるときにも資本回収係数を使うよ。
押尾：えっ！何でだろう？
みやこ：資本回収係数は、「一定期間、一定利率の利息（複利）が付くローンを借りる場合、毎回いくら返済すればよいか」を求める係数と言い換えられるよね。
押尾：わかったような、わからないような…
みやこ：とにかく、住宅ローンの返済額を求めるときには、資本回収係数を使うことだけは忘れるな！これ、絶対出るから！！
押尾：は、はい。

みやこ：年金現価係数と資本回収係数は、取り崩しグループとおぼえよう。

押尾、みやこさんのサポートをうけ、何とか6種類の係数をマスターできました（たぶん）。
つぎは問題演習だ！

6種類の係数問題演習

（問題）
浩一さんは、定年を迎えた後、公的年金の支給が始まるまでの5年間の生活資金に退職一時金の一部を充てようと思っている。仮に、退職一時金のうち500万円を年利1％で複利運用しながら5年間で均等に取り崩すこととした場合、毎年の生活資金に充てることができる金額として、正しいものはどれか。なお、下記＜資料＞の3つの係数の中から最も適切な係数を選択して計算し、解答に当たっては、万円未満を四捨五入すること。また、税金や記載のない事項については一切考慮しないこととする。

＜資料：係数早見表（年利1.0％・5年)＞

現価係数：0.95147
減債基金係数：0.19064
資本回収係数：0.20604

1) 98万円
2) 103万円
3) 108万円

2016年度1月日本FP協会（実技）

＜解き方＞
退職金を毎年いくら取り崩せるかという問題なので、資本回収係数を使います。
500万円 × 0.20604 ≒ 103万円

よって、正解は2です。

この問題は3択ですが、計算方法がわからなくても、答えを導くことができるんです。
運用利率が0％だった場合、毎年100万円を取り崩せます。
問題文では、1％で運用をしているので、100万円よりも多い額を取り崩せることがわかります。
まず、1の選択肢が消えます。

運用利率が1％の単利だった場合、1年で500万円に対し5万円の利息が付きます。
2年目は400万円に対し4万円、3年目は300万円に対し3万円…となるので、合計5年間で15万円の利息が付きます。
毎年のだいたいの取り崩し額は、515万円 ÷ 5 ＝ 103万円となり、選択肢2に一致します。

問題文は複利運用ですが、1％で5年間の複利運用では単利運用とそれほど差がありません。
係数をおぼえていなくても、算数ができれば答えがわかってしまいます。

みやこ：せっかく係数をおぼえたのに、こういう裏ワザやったら意味ないでしょ！
押尾：すみません。
みやこ：でも、試験場で頭が真っ白になった時に、こういう力技は使えるよね。
押尾：ですよね！
みやこ：とは言っても、まずは係数をしっかりおぼえること！3級はパスできても、上の級では歯が立たないよ。
押尾：ええっ！3級の先もまだやらなきゃダメですか？
みやこ：当然でしょ。

押尾のFP試験、まだまだ先が長そうです。

押尾メモ